Exemplary Info About How Do You Calculate Series Voltage

Understanding Series Voltage

1. What's the Big Deal with Series Circuits?

Ever wondered how those Christmas lights manage to twinkle so brightly? Or how your car's battery provides the power it needs? A lot of it boils down to understanding series circuits. In a series circuit, components (like resistors or light bulbs) are connected one after another, forming a single path for the electric current to flow. Think of it like a single lane road; cars (electrons) can only travel one way, sequentially passing each point. This is where calculating the series voltage becomes incredibly important. This series voltage topic is not always simple to master, but once you are, it is simple.

Why is understanding series voltage important? Because the voltage, which is the electrical potential difference, is divided among the components in the circuit. Each component gets a share of the total voltage. Figuring out how much each component gets is essential for designing safe and effective circuits. Without this knowledge, you could potentially overload components, leading to failures or even hazards. And nobody wants a Christmas tree fire, right? Understanding this concept allows for a more efficient and reliable system.

Imagine you're baking a cake. You need to know how much of each ingredient to add to get the right taste and texture. Similarly, in a series circuit, understanding how voltage is distributed is crucial for ensuring each component operates correctly. Otherwise, your circuit might end up being a "flop," just like a cake that's missing a key ingredient.

So, let's dive into the practicalities of calculating series voltage. It's surprisingly straightforward, and with a little practice, you'll be calculating voltage drops like a seasoned electrical engineer (minus the fancy hat, unless you want to wear one!). The journey to understanding electrical circuits can be a fun, rewarding one.

The Formula

2. Unlocking the Voltage Calculation Secret

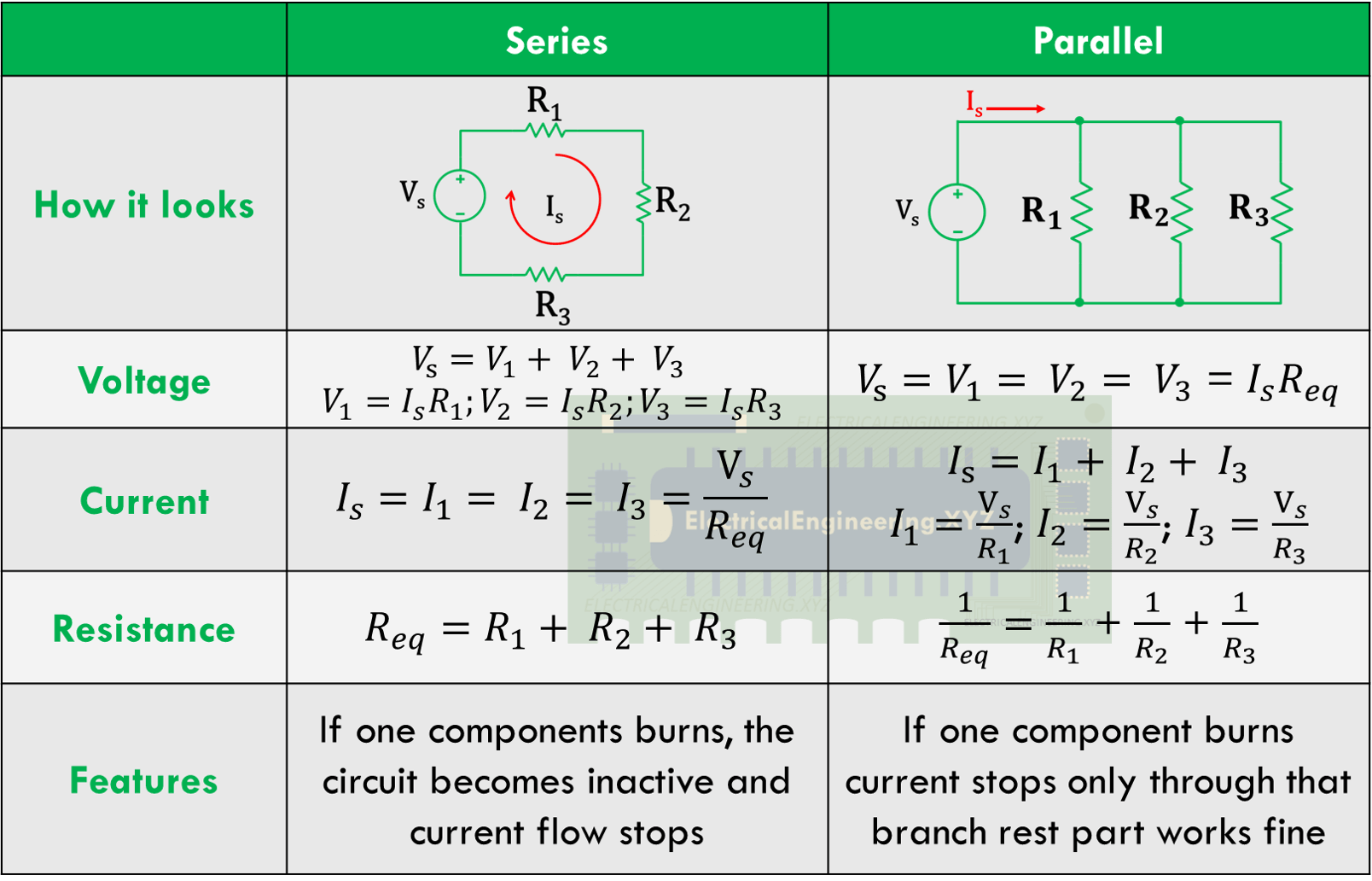
Alright, let's get to the core of the matter: the formula for calculating series voltage. The good news is that its incredibly simple: the total voltage in a series circuit is equal to the sum of the voltage drops across each individual component. Mathematically, it looks like this: V_total = V₁ + V₂ + V₃ + ... and so on. It is quite easy to imagine, is it not? This concept of series voltage is so fundamental and easy.

Think of it like this: you're going on a road trip. The total distance of your trip is equal to the sum of the distances between each stop along the way. The voltage drops are like the distances between each stop. To find the total distance, you simply add up each segment. This is a perfect analogy to understand the concept better, and it is a great way to visualize electrical systems.

Lets say you have a series circuit with three resistors. Resistor 1 has a voltage drop of 2 volts, resistor 2 has a voltage drop of 3 volts, and resistor 3 has a voltage drop of 5 volts. To find the total voltage of the circuit, you simply add them up: 2 + 3 + 5 = 10 volts. Therefore, the total voltage of the circuit is 10 volts. Simple as pie, isnt it? Calculating series voltage is easy once the underlying logic is understood.

Now, I know what you might be thinking: "This seems too easy. There must be a catch!" Well, there isn't really a catch. As long as you know the voltage drop across each component, calculating the total voltage is just a matter of simple addition. Remember, this applies specifically to series circuits where components are connected one after the other. The concept of series voltage is a beautiful part of electrical engineering, and this understanding can greatly assist in circuit building.

Applying Ohm's Law

3. Oming the situation with Ohm's Law

Sometimes, you wont be directly given the voltage drop across each component. Instead, you might be given the resistance of each component and the current flowing through the circuit. This is where Ohm's Law comes to the rescue. Ohm's Law states that Voltage (V) = Current (I) x Resistance (R), or V = IR for short. Understanding and applying Ohm's Law is essential to calculating series voltage.

In a series circuit, the current is the same throughout the entire circuit. So, if you know the current and the resistance of each component, you can calculate the voltage drop across each component using Ohm's Law. Then, once you have the voltage drops for each component, you can add them up to find the total voltage, just like we discussed earlier. It provides insight into the relationship between voltage, current, and resistance within a circuit.

For instance, imagine a series circuit with a 10-ohm resistor and a current of 2 amps. Using Ohms Law (V = IR), the voltage drop across the resistor would be V = 2 amps 10 ohms = 20 volts. If you have multiple resistors in series, you'd calculate the voltage drop across each one individually and then sum them up to find the total voltage of the source. It allows you to predict the voltage distribution throughout the circuit and ensure that each component operates within its safe limits.

Think of Ohm's Law as your trusty sidekick in the world of circuit analysis. It provides a fundamental relationship between voltage, current, and resistance that allows you to solve a wide range of circuit problems. Mastering Ohms Law is a critical step in understanding how to calculate voltage in series circuits and confidently design and troubleshoot electrical systems. This concept and formulas can be a great asset in one's electrical engineering skills.

Practical Examples: Let's Get Hands-On

4. Putting Theory into Practice

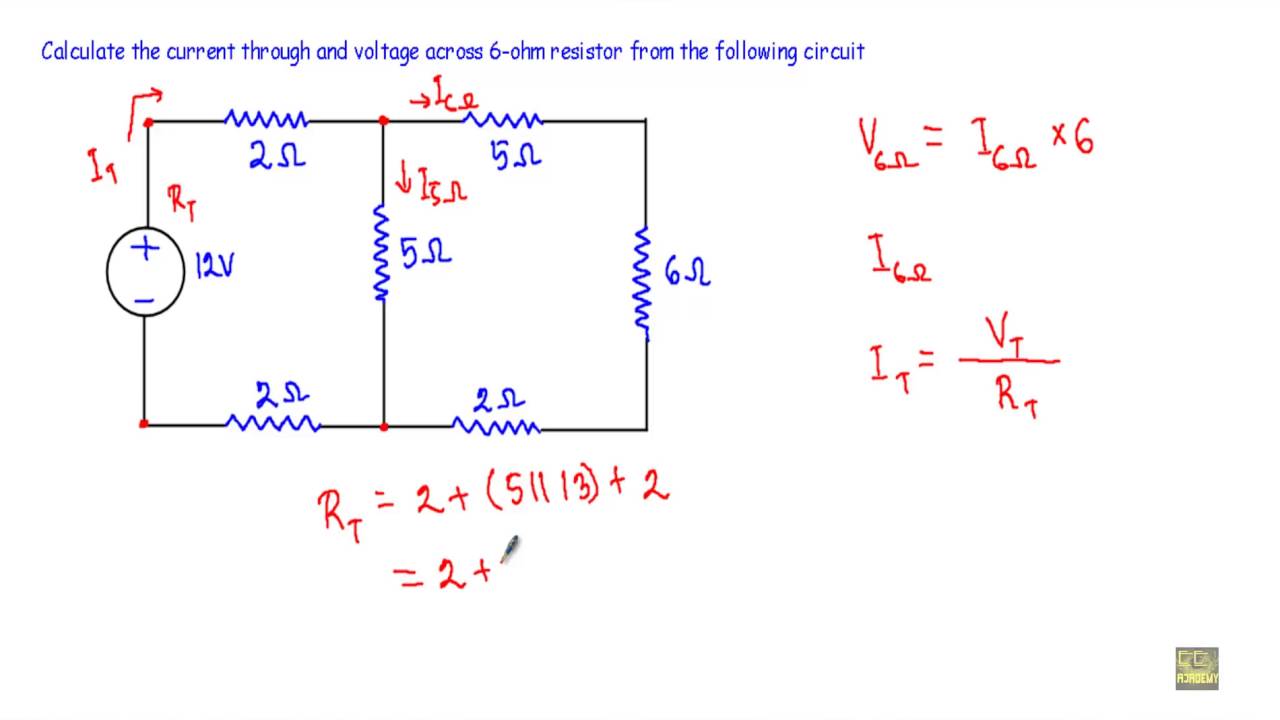
Alright, enough theory! Lets work through a few practical examples to solidify your understanding. Imagine you have a series circuit with two resistors. Resistor 1 has a resistance of 100 ohms, and resistor 2 has a resistance of 200 ohms. The current flowing through the circuit is 0.1 amps. What is the total voltage of the circuit? This example shows an excellent practical application of series voltage calculation.

First, we need to find the voltage drop across each resistor using Ohm's Law (V = IR). For resistor 1: V₁ = 0.1 amps 100 ohms = 10 volts. For resistor 2: V₂ = 0.1 amps 200 ohms = 20 volts. Now, we add the voltage drops together to find the total voltage: V_total = V₁ + V₂ = 10 volts + 20 volts = 30 volts. Therefore, the total voltage of the circuit is 30 volts. Not too difficult, right? This example provides a clear step-by-step process of calculating series voltage in a circuit.

Let's try another one. Suppose you have three light bulbs connected in series. Each light bulb has a resistance of 4 ohms, and the circuit is powered by a 12-volt battery. What is the voltage drop across each light bulb? Since the light bulbs are identical and in series, the voltage will be equally distributed across them. The current flowing through the circuit can be calculated using Ohm's Law where resistance is the sum of all resistance 4+4+4. So, the current I = V / R = 12 volts / (4 ohms + 4 ohms + 4 ohms) = 12 volts / 12 ohms = 1 amp. Each lightbulb drops 4 volts.

These examples demonstrate that you can also determine each element series voltage, and understand your electrical circuit. By working through these examples, youll gain confidence in your ability to apply the concepts weve discussed and solve real-world circuit problems. Practice makes perfect, so keep practicing, and youll become a series circuit master in no time!. It is a very crucial thing to take into account.

Common Mistakes to Avoid

5. Steering Clear of Pitfalls

Even with a simple formula, there are some common mistakes that people make when calculating series voltage*. One of the biggest mistakes is forgetting that the current is the same throughout the entire series circuit. This is crucial for applying Ohm's Law correctly. If you assume the current is different for each component, your calculations will be way off. This is a common mistake that can lead to incorrect results.

Another common mistake is confusing series circuits with parallel circuits. In a parallel circuit, the voltage is the same across each branch, but the current is divided. Using the series voltage formula on a parallel circuit will give you incorrect results. It is important to know what kind of circuit it is, and if you do not know, determine first. It's important to differentiate between series and parallel circuits.

Also, pay attention to units! Make sure you're using the correct units for voltage (volts), current (amps), and resistance (ohms). Mixing up units will lead to incorrect calculations. Always double-check your units before plugging them into the formula. If you do not double check, your calculation will be wrong. Not taking into account the units used, such as kilo vs mili.

Finally, double-check your work! It's easy to make a simple arithmetic error, especially when dealing with multiple components. Take a few extra seconds to review your calculations to ensure they are accurate. This can save you a lot of headaches and prevent potential problems in your circuit design. Avoiding these common mistakes will help you calculate series voltage with confidence and accuracy. It is always important to check your work to make sure they are right.